Korekta zaznaczona na żółto
Wiele moich przekształceń jest robiona intuicyjnie zgodnie z moją wiedzą i dobrą wolą, zgodnie z zasadą że co nie jest zabronione jest dozwolone. Na razie nie umiem w pełni wyprowadzić tych wzorów dlatego też możliwe jest że istnieją rzeczy które przeoczyłem a które mogą zmieniać końcowy wynik. Ta technika „na pałę” zapewne u wielu osób zajmujących się tym na co dzień może być szokiem i uważana jest za "barbarzyństwo", jednak dla mnie o wiele bardziej ważna jest skuteczność od poprawności i eleganckich rozwiązań. Nie znam przyczyn dlaczego moje przekształcenia miały by być błędne dlatego uważam je za prawdziwe. Jeżeli prawdziwe jest stwierdzenie że M=Iω2 to takie stwierdzenie jest dla mnie również prawdziwe Ixɛx = Iyωyωz – Izωzωy = Mx . Mimo że jak do tej pory słyszałem mnóstwo opinii że tak nie można to jednak nikt jeszcze nie podał mi dowodu na błąd tego stwierdzenia.
Interpretacja geometryczna wzorów Eulera.
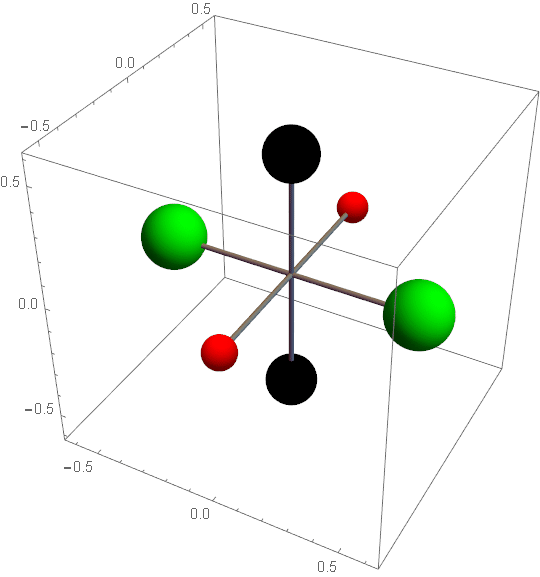
Moment bezwładności to
Momenty bezwładności możemy uzyskać na różne sposoby na przykład aby uzyskać I=4 możemy zastosować r=1 i m=4 lub r=2 i m=2.
Aby wyznaczyć moment bezwładności BS względem osi należy zsumować momenty bezwładności wszystkich punktów materialnych BS względem tej osi
I=∑miri2 (1)
gdzie r jest promieniem do osi obrotu.
Chcemy ustalić trzy główne momenty bezwładności BS na Ix=2, Iy=4, Iz=6. (2)
Aby uprościć przekaz załóżmy że wszystkie ramiona
Aby uzyskać nasze założenia:
na osi x mamy dwie masy po 1
na osi y mamy dwie masy po 2
na osi z masy równe są zero.
Zgodnie ze wzorem (1)
Ix=2(my*r)+2(mz*r)=4+0 (4)
Iy=2(mz*r)+2(mx*r)=0+2
Iz=2(mx*r)+2(my*r)=4+2
Moje przekształcenia wzorów Eulera wyglądają następująco:
Ixɛx = Iyωyωz – Izωzωy + Mxz = Mx (5a)
Iyɛy = Izωzωx – Ixωxωz + Myz = My
Izɛz = Ixωxωy – Iyωyωx + Mzz = Mz
Mxz ; Myz ; Mzz -Momenty sił zewnętrznych w naszym przypadku równe są zero. Mamy więc
Ixɛx = Iyωyωz – Izωzωy = Mx (5b)
Iyɛy = Izωzωx – Ixωxωz = My
Izɛz = Ixωxωy – Iyωyωx = Mz
Musimy teraz przyjąć współrzędne wektora prędkości kątowej Ω. Zauważmy że jeżeli wektor Ω ma tylko jedną współrzędną niezerową to wszystkie równania równe są zero. Nasz wektor ma następujące współrzędne
Ω=(-1/2; -√3/2; 0) czyli ωx=1/2; ωy=√3/2; ωz=0 czyli Ω=1 (6)
Podstawiamy do wzorów (5), w dwóch pierwszych równaniach mamy ωz=0 więc będą one równe zero
Mx=0 (7)
My=0
Mz= √3 - √3/2 = √3/2
ɛz = √3/12
Moment siły jest to iloczyn wektorowy
M = r x F (8)
Wiemy że moment siły leży na osi z, pytanie jest na których osiach leżą r i F. Wyjaśni się to gdy zrozumiemy działanie wahadła stożkowego.
https://pl.wikipedia.org/wiki/Wahad%C5%82o_sto%C5%BCkowe
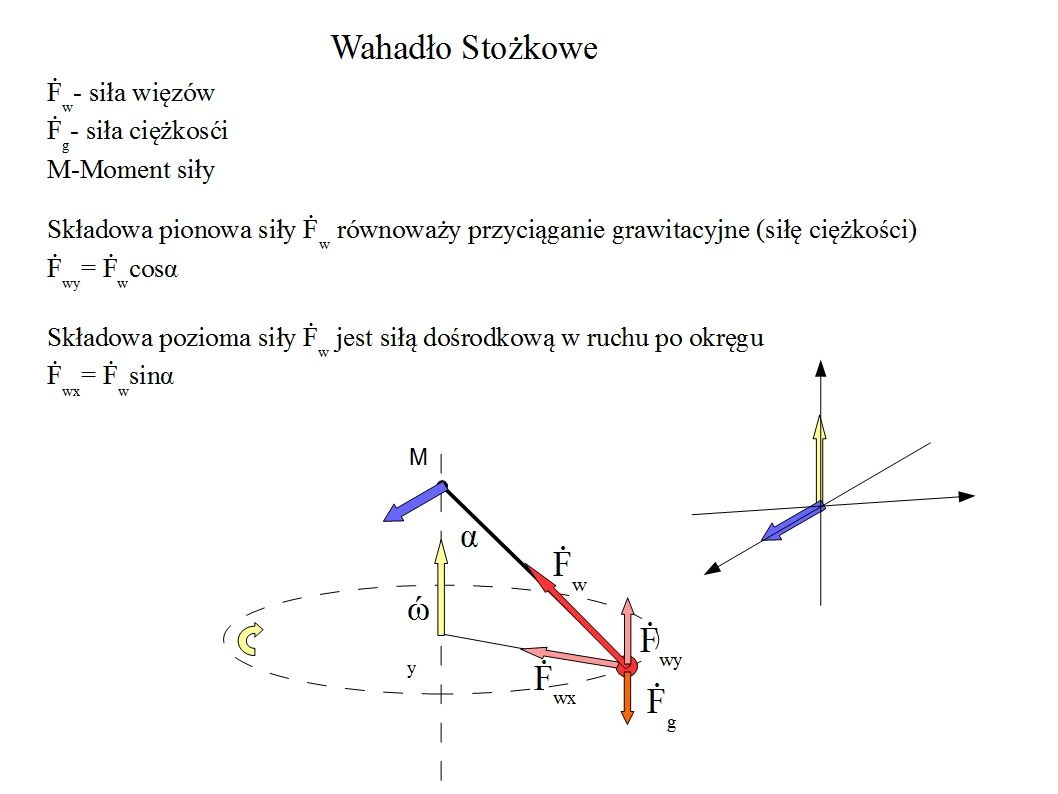
Umieszczając ciężarek na ramieniu (wahadło) i wprowadzając go w ruch obrotowy obserwujemy podnoszenie się ciężarka, czyli wychylenie ramienia z pozycji pionowej o pewien kąt. Zjawisko to tłumaczy się działaniem siły więzów które rozchodzą się wzdłuż ramienia. Ponieważ ramie jest nachylone pod pewnym kątem α to siła więzów ma dwie składowe.
Składową poziomą Fwx=sinα oraz (9)
Składową pionową Fwy=cosα
Siła Fwy uważa się za odpowiedzialną za zjawisko unoszenia ciężarka. W polu grawitacyjnym wahadło podnosi się lub opada do momentu kiedy siła Fwy zrówna z siłą ciążenia Fg.
Ciekawa obserwacja:
Składowe pionowe siły więzów zawsze pchają ciężarek do wychylenia o 90 stopni. Przy wychyleniu tym wahadło posiada największy moment bezwładności, jednocześnie składowa pionowa siły więzów równa jest zero. Składowa pionowa siły więzów jest przyczyną dążenia BS do największych momentów bezwładności. Do tej pory nikt nie potrafił wytłumaczyć co jest tego przyczyną.
Definicja:
Stan równowagi wahadła stożkowego w polu grawitacyjnym jest to stan w którym składowa pionowa siły więzów jest równa sile ciążenia.
Fwcosα=mg
Nie mylić ze stanem równowagi wahadła Fizycznego, gdzie stan równowagi jest wtedy gdy energia potencjalna jest najmniejsza. W wahadle stożkowym jak i w efekcie Dzanibekowa nie mamy do czynienia z klasyczną oscylacją wokół punktu równowagi jaką znamy z wahadła Fizycznego.
Ważne pytania na które nie znam jeszcze odpowiedzi:
Ile czasu potrzebuje wahadło stożkowe by z pozycji startowej uzyskać stan równowagi?
Po jakiej trajektorii będzie się poruszać?
Jak zachowuje się wahadło stożkowe poza polem grawitacyjnym? Czy podlega ono wtedy nutacji?
Wyliczanie składowej pionowej siły więzów Fw.
Obecna interpretacja zakłada że siła dośrodkowa Fd musi być prostopadła od wektora prędkości kątowej i działa ona wzdłuż promienia do osi obrotu r, czyli zgodnie ze wzorem
ω= R x v (10)
Fwx=Fd
Składowa pozioma siły więzów jest równa sile dośrodkowej odpowiedzialnej za prędkość kątową ω. Te założenia (10) powodują pewne komplikacje, wzór na siłę dośrodkową to
Fwx=-mω2R (11)
R jest to promień do osi obrotu czyli R=sinαr.
Zakładając punkt (10) i (9) jest prawdziwy to
Fw 2= Fwx2 + Fwy 2 (12)
załóżmy że m=1; r=1 i ω=1 stosując wzór (11) daje nam to
Fw = √(sinα2+ cosα2)=1 (13)
Świadczyłoby to o tym że siła więzów jest niezależna od kąta wychylenia ramienia. Stąd też pewnie się bierze obecnie przeświadczenie że siły więzów nie mają wpływu na mechanikę bryły sztywnej. Zadziwiające że siła więzów jest taka sama przy wychyleniu 0, 45 i 90 stopni. Nie podoba mi się ta interpretacja. Spójrzmy na to trochę inaczej. Po prostu zsumujmy składową pionową i składową poziomom siły więzów i mamy wtedy zgodnie z założeniami z punktu (12)
Fwx+ Fwy = sinα + cosα (14)
Dla kąta 45⁰ stopni mamy √2 ale dla kąta -45⁰ mamy zero. Dla kąta 0⁰ mamy 1 tak samo jak dla kąta 90⁰. dla kątów 30⁰ i 60⁰ mamy tą samą wartość (1+√3)/2 ale dla kąta -30⁰ mamy 1-(√3/2)a dla kąta -60⁰ (√3/2)-1. Kiedy wahadło wychyla się o 45⁰ a kiedy o -45⁰?
W mojej metodzie która jest bardzo kontrowersyjna nie mamy tego typu problemów. Zakładam że siła dośrodkowa rozchodzi się wzdłuż ramienia r a nie prostopadle do osi obrotu. Co to zmienia? Koryguje wzór (11) który według mnie jest wzorem na całkowitą siłę dośrodkową korekta punktu (10)
Fw=Fd (15)
Fw=-mω2sinαr
Teraz wzór na składowe poziomą i pionową siły więzów.
Fwx=-mω2 sinα sinαr (16)
Fwy=-mω2 sinα cosαr
Co to zmienia? Teraz dla kąta 0⁰ nie mamy sił więzów, wychylenie dodatnie i ujemne są symetryczne czyli wychylenia α i -α dają te same wartości, przy wychyleniu o 90⁰ i -90⁰ czyli z największym momentem bezwładności nie ma składowych pionowych sił więzów. Kierunek działania składowej pionowej siły więzów zmienia się co 90⁰co odpowiada zachowaniu wahadła stożkowego. Teraz siła wskazuje kierunek poruszania się wahadła zgodnie z jego zachowaniem w rzeczywistości.
Wykres funkcji sin, cos, sin+cos i sincos.
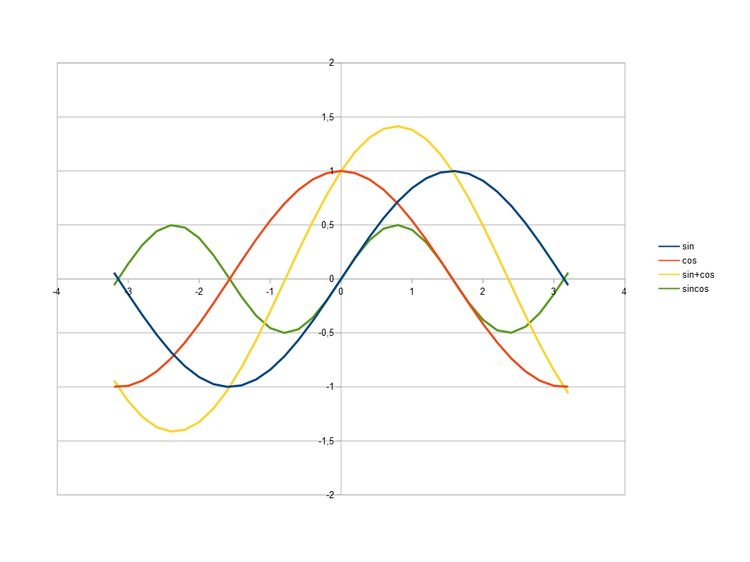
Po zsumowaniu tak wyliczonych sił w BS otrzymamy takie same wyniki jak z równań Eulera. Równania Eulera najwygodniej jet badać w układzie współdłużnych BS gdzie osie główne pokrywają się z głównymi osiami bezwładności. Czyli w układzie gdzie nasze kulki znajdują się na osiach głównych.
Wróćmy teraz do naszego modelu BS z punkt (3)(6). Każde z ramion jest osobnym wahadłem stożkowym i teraz trzeba umieć poskładać te ramiona w całość
Bierzemy jedną oś BS i rozpatrujemy tylko jedną masę z osi x, pamiętając że na osi tej znajduje się druga symetryczna masa r=1; m=1
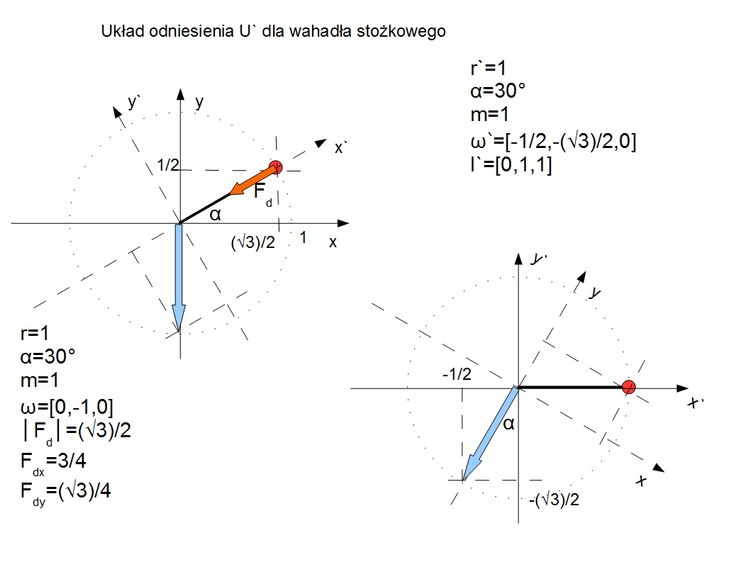
Stosując wzór (16) mamy
Fwy1= √3/4
Pamiętamy że na osi znajduje się druga masa po przeciwnej stronie której składowa pionowa siły więzów daje ten sam moment siły. Czyli uzyskany wynik mnożymy razy 2.
Fwy1= √3/2 (17)
Przypomnijmy teraz ostatnią linijkę wzoru (5)
Izɛz = Ixωxωy – Iyωyωx = Mz
Nasze Fwy1 pasuje idealnie do członu Iyωyωx .
Teraz rozrysujmy jak będzie działało wahadło stożkowe gdy połączymy je na sztywno z drugim wahadłem stożkowym pod kątem prostym. W naszym obrocie gdzie na jednej płaszczyźnie znajdują się obydwa ramiona i wektor prędkości kątowej, składowe pionowe sił więzów obydwu ramion będą przyczyną zaistnienia przeciwnych momentów sił. Czyli należy je odjąć.
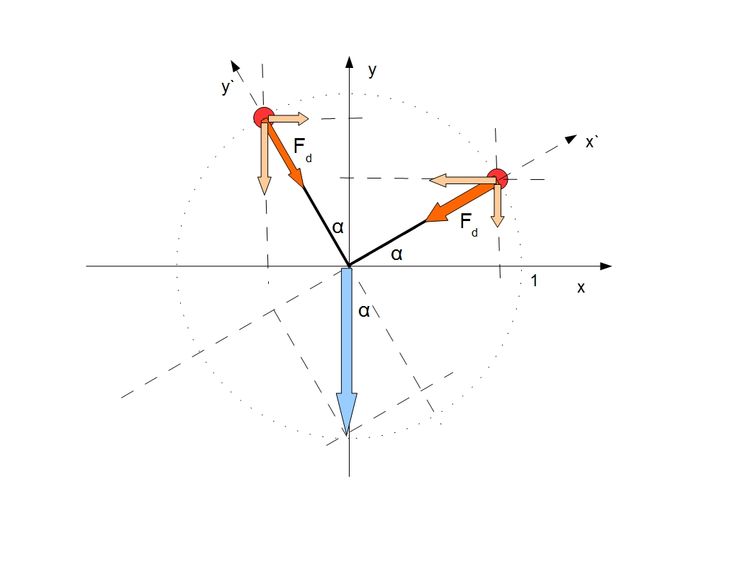
Sprawdzając teraz Fwy2 drugiego ramienia z masą na osi y biorąc pod uwagę obydwie masy otrzymujemy
Fwy2 = √3 (18)
I znowu ten element idealnie pasuje do wzoru(5) Fwy2 =Ixωxωy . I dokładnie jak we wzorze (5) siły te są przeciwstawne.
Na tyle na ile umiałem na tyle sprawdziłem i wszystko co sprawdzam zgadza się idealnie. Mamy końcowy wzór na wyliczenie siły kręcącej naszą BS.
Izɛz = ωy x Ixωx – ωx x Iyωy = Mz
Jak to działa pokazuje ten schemat.
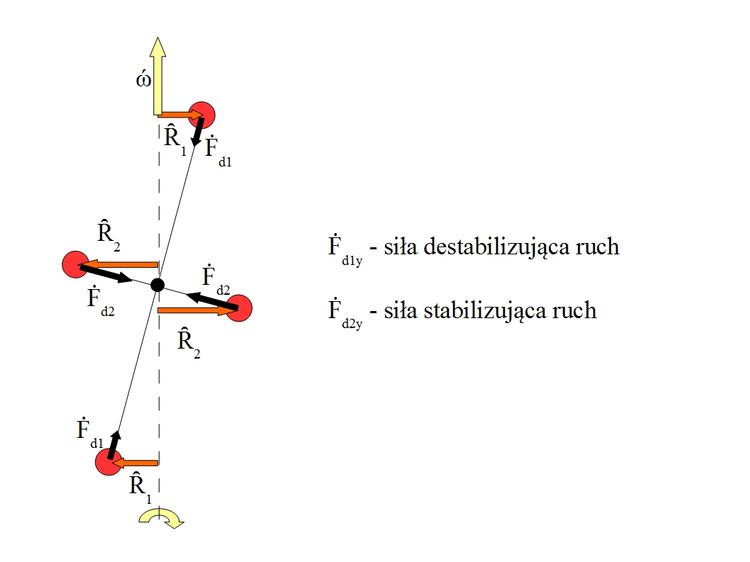
Każde ramie jest pchane przez składową siły więzów do swojego największego momentu bezwładności. Ramiona przepychają się nawzajem a wypadkowa działania tych sił określa przyspieszenie kątowe BS.
Wersja wstępna, może ulec korekcie.









Komentarze
Pokaż komentarze (1)