Na wstępie sprostowanie.
Cała mechanika obrotu BS jest dość złożona, składa się z wielu detali a diabeł jak zawsze tkwi w szczegółach. Często przegapienie jakiegoś szczegółu lub zła jego interpretacja wywraca nam wszystko do góry nogami.
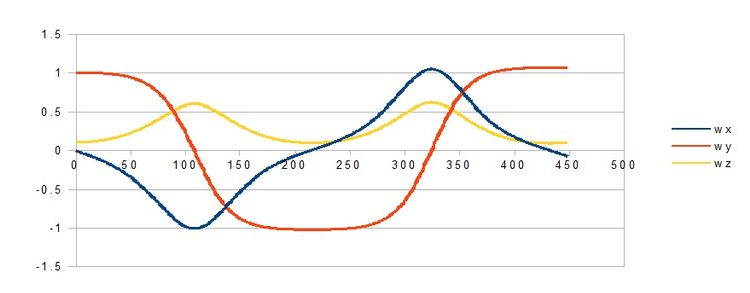
Jeden z czytelników uparcie twierdził że podczas efektu Dżanibekowa dochodzi do zmiany kierunku obrotu, no i chyba ma racje. Przy starcie wx=0; wy=1; wz=0,1 jak pokazuje wykres składowych wektora omegi zarówno wx jak i wy zmieniają znak na przeciwny, czyli dochodzi do zmiany kierunku obrotów.
 Podziękowania dla KK-51 za konsekwentne wskazywanie tego detalu.
Podziękowania dla KK-51 za konsekwentne wskazywanie tego detalu.
Przechodząc do tematu. Jak do tej pory wyznaczałem pozycje wektorów w układzie BS gdzie Ix, Iy i Iz są stałe w czasie, jednak co tu wiele mówić nikt chyba nie potrafi odnieść tego do inercjalnego układu czyli tego jak my to widzimy. Sprawa jest dość skomplikowana gdyż musimy dokonać złożonych obrotów od których łatwo może się zakręcić w głowie.
Na początek parę słów jak działa program. Program wykonuje działania skokowo, wyliczane są parametry w czasie dt a następnie dochodzi do przemieszczenia współrzędnych o krok dt i na podstawie nowych współrzędnych wyliczany jest krok następny.
W czym problem? Program musi dokonać zaokrągleń wyników, Vpython chyba do 15 miejsca po przecinku. Przy kilku krokach nie ma to żadnego znaczenia ale jeżeli kroków jest kilka tysięcy to zaokrąglenia mogą zacząć się mnożyć niczym nasze odsetki od kredytu. Z każdym następnym krokiem błąd się powiększa, dlatego ważne jest aby minimalizować kroki algorytmów do jak najkrótszych, gdyż im jest krótszy tym większe szanse że jest bardziej dokładny. Przy obrotach ważny jest też odcinek czasu dt, im mniejsze dt tym dokładniej program wylicza współrzędne.
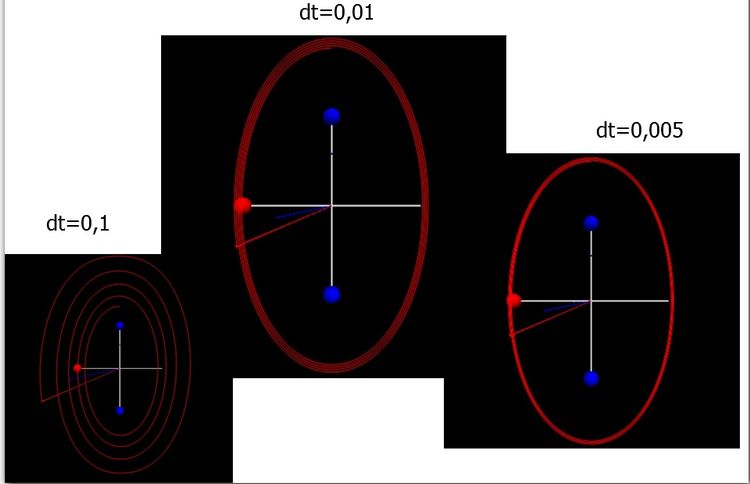
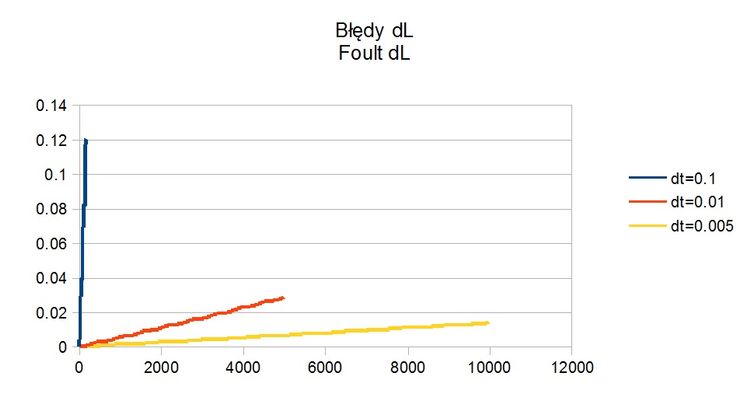
Jednak w poniższej symulacji musimy wyliczyć zmianę kąta pomiędzy wektorami i pojawia się kolejny problem. Przy bardzo małym dt mamy do czynienia z bardzo małymi kątami przemieszczenia a im mniejsza liczba tym większy błąd zaokrąglenia. Prawdę mówiąc krokowe przesunięcia kąta nie ma większego sensu gdyż przy małym dt będziemy mieli duży błąd wyliczenia współrzędnych obrotu a przy mały dt duży błąd wyliczaniu kątów.
Dlatego tez zastosowałem pewien magiczny trik. Moje symulacje w układzie BS są bardzo stabilne, błąd przy pełnym obrocie czasami jest mniejszy od 1/1000 dlatego też współrzędne te stanowią bazę do późniejszych wyliczeń. Na animacji wyliczeń tych nie widać.
Tak jak pisałem wcześniej ważne jest aby zminimalizować algorytm do jak najmniejszej ilości kroków, dlatego zastosowałem drugi magiczny krok który pozwolił mi ominąć skomplikowane wyliczenia i ograniczyć działania do sześciu linijek. Cztery są niezbędne do wyliczenia dwóch niezbędnych wektorów a następnie dokonujemy dwóch obrotów.
Wykorzystałem fakt że L i L` mają taka samą długość, odejmując te wektory otrzymamy wektor A który kiedy umieścimy na L` wskaże nam L
A=L`-L
Ponieważ trójkąt L, L`, A jest trójkątem równoramiennym A/2 wskaże nam wektor który będzie dwusieczną kąta
O=L`+A/2
Następnie obracamy naszą Ω` o 180 stopni dookoła O
W=w.rotate(axis=O, angle=pi)
Ale wtedy nasza omega jest po przeciwnej stronie L, więc drugim obrotem umieszczamy ją na właściwym miejscu
W=W.rotate(axis=L, angle=pi)
W ten sposób mamy wektor Ω który jest nachylony do L pod tym samym kątem i kierunkiem co Ω` do L`. Za każdym razem wyliczane jest Ω na bazie współrzędnych Ω` do L`. Dodatkowo obliczyłem osobno kąty <ΩL i < Ω`L` i odjąłem je od siebie wyliczając w ten sposób błąd metody. Jak to pokażą wykresy jest on największy przy bardzo małych kątach jednak nie zakłóca on znacząco wyniku.
Poniżej filmik z większą ilością detali.
Wykres zmian kątów w stopniach
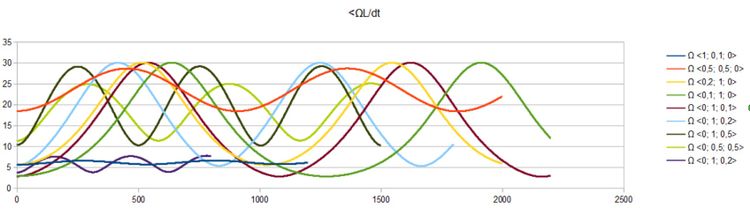
oraz bardzo ciekawe trajektorie pozycji Ω do sztywnego L
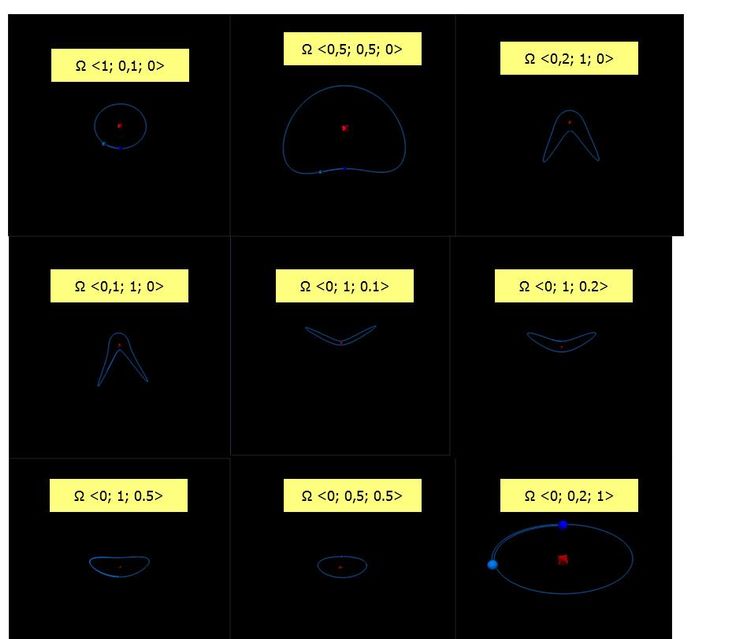
Teraz trzeba wymyślić algorytm dla następnych obrotów aby móc w końcu zobaczyć efekt Dżanibekowa w każdym nawet najmniejszym detalu.
from visual import *
Ix=1.
Iy=2.
Iz=3.
wx=0
wy=1
wz=0.1
ex=((Iy-Iz)*wy*wz)/Ix
ey=((Iz-Ix)*wz*wx)/Iy
ez=((Ix-Iy)*wx*wy)/Iz
lx=wx*Ix
ly=wy*Iy
lz=wz*Iz
L=vector(lx,ly,lz)
W=vector(wx,wy,wz)
#print lx,ly,lz
#kropkaw=sphere(pos=vector(wx,wy,wz), radius=0.01, color= color.blue, make_trail=True)
kropkawprim=sphere(pos=vector(wx,wy,wz), radius=0.01, color= (0,0.5,1), make_trail=True)
kropkak=sphere(pos=vector(lx,ly,lz), color= color.red, radius=0.01, make_trail=True)
omega=arrow(axis=vector(0,0.01,0), color= color.blue, shaftwidth=0.01)
kret=arrow(axis=vector(lx,ly,lz), color= color.red, shaftwidth=0.01)
kretprim=arrow(axis=vector(lx/3,ly/3,lz/3), color= color.red, shaftwidth=0.01)
os=arrow(axis=vector(0,0.1,0), color= color.green, shaftwidth=0.01)
dt=0.01
t=0
while t<200:
rate(100)
ex=((Iy-Iz)*wy*wz)/Ix
ey=((Iz-Ix)*wz*wx)/Iy
ez=((Ix-Iy)*wx*wy)/Iz
wx=wx+ex*dt #wspolrzedne omegi
wy=wy+ey*dt
wz=wz+ez*dt
mx=ex*Ix #moment sily
my=ey*Iy
mz=ez*Iz
lx=wx*Ix
ly=wy*Iy
lz=wz*Iz
l=vector(lx,ly,lz)
w=vector(wx,wy,wz)
lr=l-L
O=L+(lr/2)
a=diff_angle(l,L)
b=diff_angle(w,l)
W=w.rotate(axis=O, angle=pi)
W=W.rotate(axis=L, angle=pi)
c=diff_angle(W,L)
d=(c-b)
print t, degrees (b), degrees(d)
# omega.axis=vector (wx,wy,wz)
omega.axis=vector (W.x,W.y,W.z)
kretprim.axis=vector(lx/3,ly/3,lz/3)
os.axis=vector(O.x/3,O.y/3,O.z/3)
# kropkaw.pos=vector(wx,wy,wz)
kropkawprim.pos=vector(W.x,W.y,W.z)
# kropkak.pos=vector(lx/3,ly/3,lz/3)
t=t+1

