Niektórzy twierdzą że zachowanie się swobodnego punktu materialnego niewiele ma wspólnego z zachowaniem się punktu "uwięzionego" w bryle sztywnej. Pozwolę się z tym stwierdzeniem nie zgodzić.
Bryłą sztywną nazywa się układ wielu (na ogół) punktów materialnych, których wzajemne odległości pozostają stałe. W moim założeniu każdy punkt ma swój wektor prędkości, położenia i działające na dany punkt siły będący przyczyną zmiany dv/dt. Aby w pełni poznać mechanikę obrotu bryły sztywnej, w mojej opinii należy dokładnie opisać mechanikę pojedynczego punktu a następnie należy znaleźć poprawny sposób sumowania (łączenia) punktów w bryłę sztywną.
Moim celem jest znalezienie wektora przyspieszenia zarówno a jak i ɛ, na podstawie których będzie można w prosty sposób wyliczyć zarówno kierunek jak i dynamikę zmian obu prędkości. Pozwoli to w mechanice BS zastąpić obecnie stosowane skomplikowane transformacje macierzy jednym wektorem i jednym wzorem. Pozwoli to na przyswojenie tej wiedzy osobom bez specjalistycznego wykształcenia oraz powinno ujawnić zależności jak do tej pory dla ludzkości nie widoczne.
Ja nie tworzę rzeczywistości ja ją odkrywam.
Największe kontrowersje mojego rozwiązania budzi zdefiniowany przez zemnie moment siły wewnętrznych. Podobno według obecnej wiedzy istnienie momentu siły musi skutkować zmianom wektora krętu L w końcu dL/dt=M. Ale czy oby na pewno? Jak za chwilę przedstawię jest to tylko intuicyjne przypuszczenie które mija się z prawdą.
Aby było łatwiej bierzemy ramię gdzie na końcach znajdują się dwie jednakie masy. Bryła ta posiada prędkość kątową Ω której wektor nie jest równoległy do żadnej z osi głównej. Dostaniemy stan BS gdzie kręt L będzie nachylony do wektora Ω pod pewnym kątem. Jak to się robi pokazuje niezawodna profesor Popko.
Aby lepiej zilustrować rozkład wektorów bryły sztywnej w pewnym konkretnym stanie, stworzyłem schemat który pokazuje istotne szczegóły.
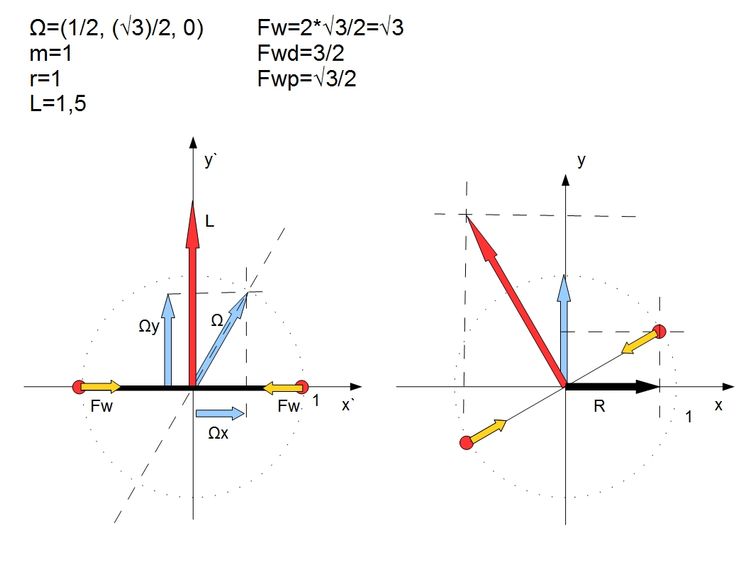
Najważniejszym szczegółem jest fakt że siły więzów Fw zawsze są skierowane prostopadle do wektora krętu L, jednocześnie gdy Ω nie jest równoległa do L siły te nie są prostopadłe do wektora prędkości kątowej. Stosując wzór na zmianę wektora krętu
dL/dt = r x Fw (1)
Okazuje się że siły więzów które są zawsze równoległe do wektora r czyli ramienia, są dla L neutralne. Siła ta nie działa na L.
A jak ta sama siła dział na wektor prędkości kątowej?
Ω = R x v (2)
Przy czym R jest to sinus kąta a nachylenia ramienia do osi prostopadłej do Ω czyli
R=sina*r (3)
Pamiętając że siła więzów rozchodzi się wzdłuż ramienia r wiemy że wzór na siłę dośrodkową to
Fw=m Ω^2R (4)
Dlatego też wstawiając wzór (3) do wzoru (4) uzyskujemy po raz kolejny na moim blogu siłę więzów równą
Fw=mrΩ^2sina (5)
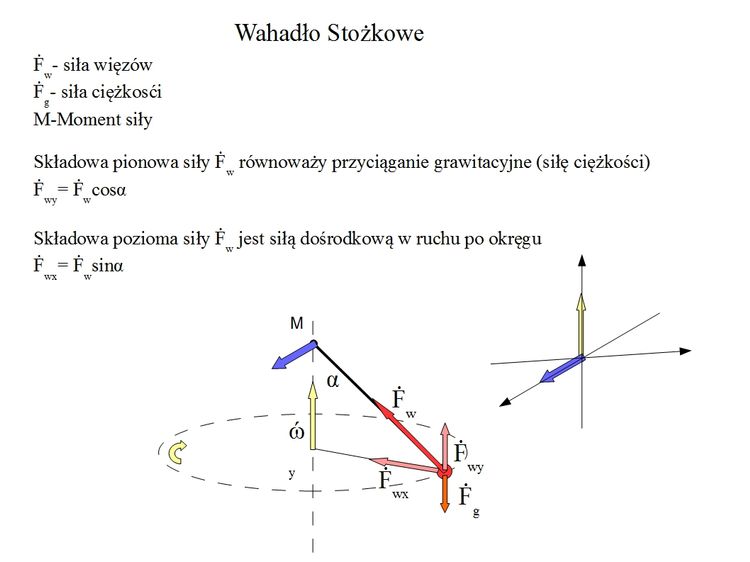
Ponieważ mój blog może mieć nowych czytelników dlatego też przypomnę że mamy w ten sposób model wahadła stożkowego. Ze wzorami na składową poziomą (dośrodkową) Fd i składową pionową Fp naszej sił więzów Fw (4).
Fwd = Fw*sina = mrΩ^2sinasina (6)
Fwp = Fw*cosa = mrΩ^2sinacosa (7)
Składowa pozioma Fwd jest więc prostopadła do wektora Ω ale ważna obserwacja, stanowi on jedynie sina siły dośrodkowej Fw. Mamy więc do czynienia z deficytem siły dośrodkowej Fd. Ponieważ wzory na przyspieszenie dośrodkowe ad to
ad=-rΩ^2 oraz (8)
ad=Fd/m
otrzymujemy wzór na Ω1 w zależności od działającej siły dośrodkowej
Ω1=√(Fd/(mr)) (9)
Na osi Ω wystąpi kątowe przyspieszenie wsteczne ɛ związane z deficytem siły dośrodkowej
ɛ=(Ω1-Ω)/dt (10)
Ale mamy jeszcze drugą składową siłę Fwp (7) która do Ω jest równoległa i która z punktu widzenia Ω a do Ωx prostopadła i
daje moment siły M.
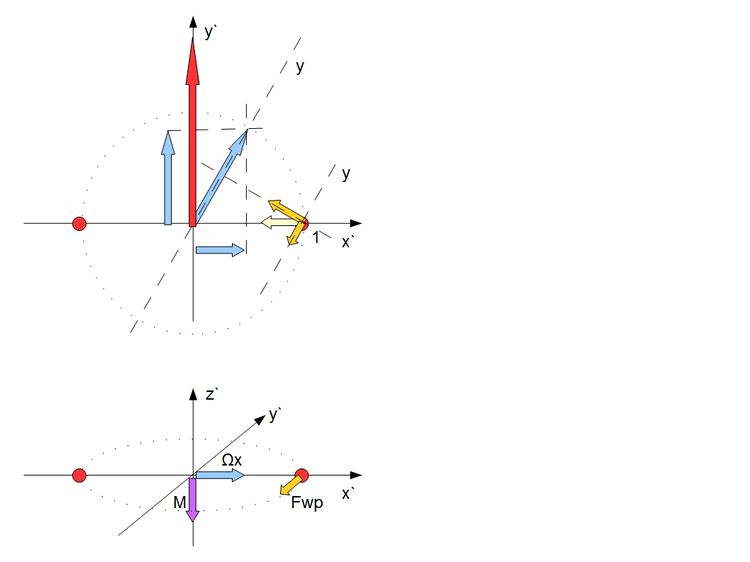
Ustanówmy teraz układ odniesienia gdzie wektor L leży na osi y a Ω leży na płaszczyźnie xy i jest nachylona do L pod kątem a który jest zarazem kątem nachylenia ramienia do osi prostopadłej do Ω. Teraz:
Ωy= Ω*cosa (11)
Ωx= Ω*sina
Okazuje się że Ω1 (10) wynikająca z siły Fwd (6) daje ten sam wynik co Ωy (11) a moment siły M wynikający z siły Fwp (7) daje siłę która jest taka sama co do wartości co siła dośrodkowa Fd (9) wynikającej z Ωx (11).
Znając wzory na iloczyn wektorowy
c = a x b (12)
c= ab*sina
Rozpędziłem się za bardzo. poniższy fragment prawdopodobnie błędny.
Okazuje się ze moje przypuszczenia dotyczące bazy do wyprowadzeń wzorów Eulera są poprawne
Idw/dt + w x Iw = D (13)
Iw=L
Zakładając że nie występują momenty sił zewnętrznych D=0, to dla naszego układu (11) poprawny jest wzór
Ω x L = Ωx x L = M (14)
Nie ma większego zaskoczenia wzory Eulera są wzorami na moment siły.
Mam w końcu siłę która nie powoduje zmiany wektora krętu L, jednocześnie dla wektora prędkości kątowej Ω wywołuje moment siły M który jest do niego prostopadły i to wszystko w pełni zgodne i bez żadnych sprzeczności z obecnym stanem wiedzy.
Bezpośrednie zastosowanie wzorów Eulera nie sprawdza się, gdyż powodują one zmianę dL/dt. Trzeba będzie je uzupełnić i odseparować moment siły powodujący zmianę wektora krętu i pozostawić jedynie ten który jest odpowiedzialny za zmianę wektora Ω.
W ten oto sposób, pokazuje nam się jak do tej pory dobrze się ukrywający, główny podejrzany o całe te figlarne fikołki. Teraz trzeba mu jeszcze udowodnić winy.
Następnym krokiem jest znalezienie rozwiązania dla zmiany dΩ/dt w stosunku do zależności Ω x M, następnie zastosować formułę do ramienia przedstawionego powyżej i ostatnim krokiem jest znalezienie formuły do połączenia ze sobą trzech prostopadłych do siebie ramion.
Jestem już tak blisko ale wciąż jeszcze tak daleko:)

